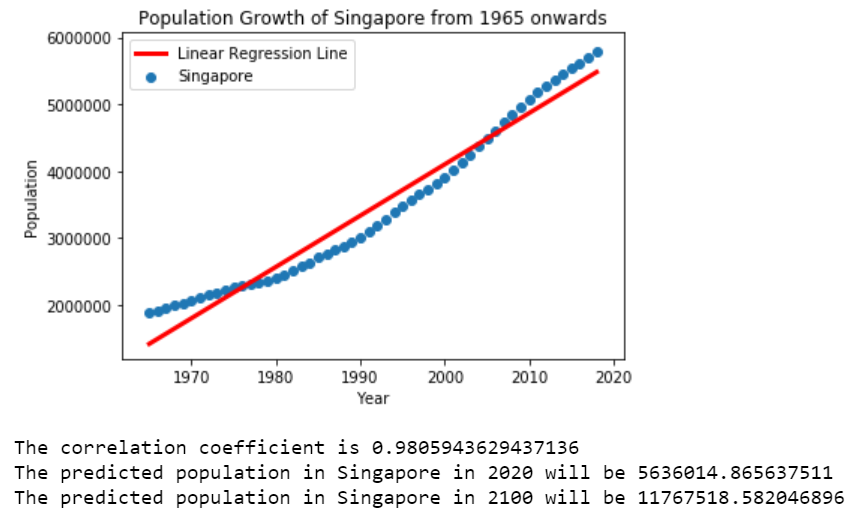
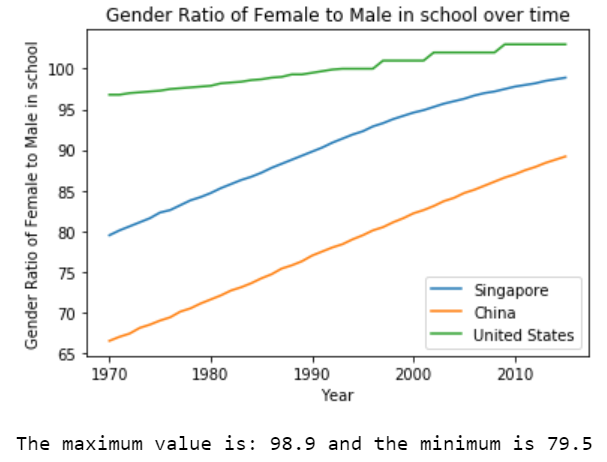
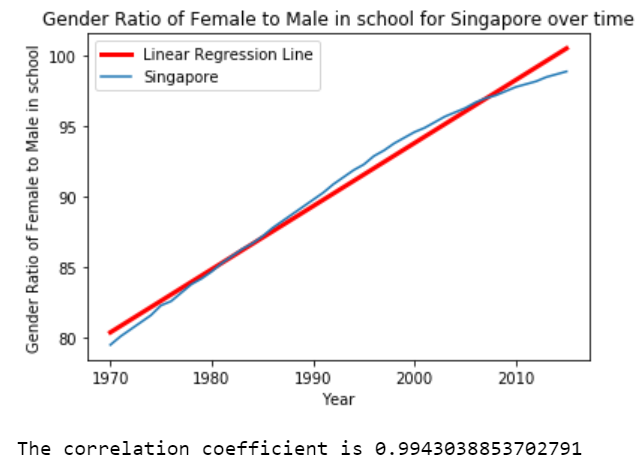
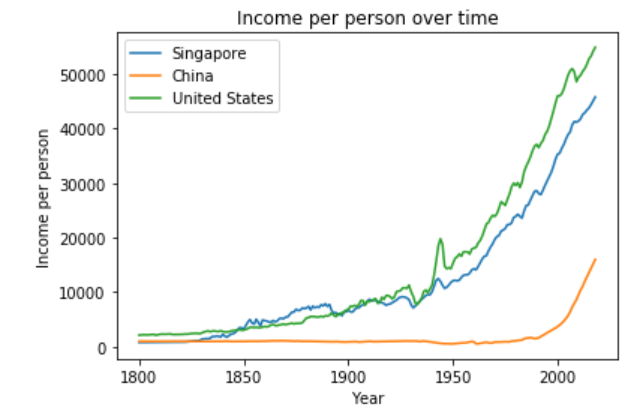
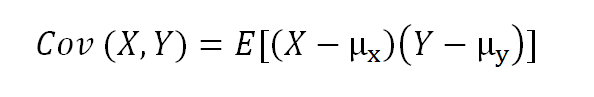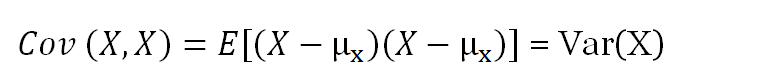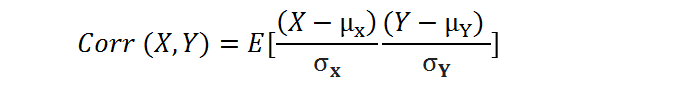Statistics is a building block of data science

Data science is an interdisciplinary field. One of the building blocks of data science is statistics. Without a decent level of statistics knowledge, it would be highly difficult to understand or interpret the data.

Statistics helps us explain the data. We use statistics to infer results about a population based on a sample drawn from that population. Furthermore, machine learning and statistics have plenty of overlaps.

Long story short, one needs to study and learn statistics and its concepts to become a data scientist. In this article, I will try to explain 10 fundamental statistical concepts.

1. Population and sample

Populationis all elements in a group. For example, college students in US is a population that includes all of the college students in US. 25-year-old people in Europe is a population that includes all of the people that fits the description.

It is not always feasible or possible to do analysis on population because we cannot collect all the data of a population. Therefore, we use samples.

Sampleis a subset of a population. For example, 1000 college students in US is a subset of “college students in US” population.

2. Normal distribution

Probability distribution is a function that shows the probabilities of the outcomes of an event or experiment. Consider a feature (i.e. column) in a dataframe. This feature is a variable and its probability distribution function shows the likelihood of the values it can take.

Probability distribution functions are quite useful in predictive analytics or machine learning. We can make predictions about a population based on the probability distribution function of a sample from that population.

Normal (Gaussian) distribution is a probability distribution function that looks like a bell.

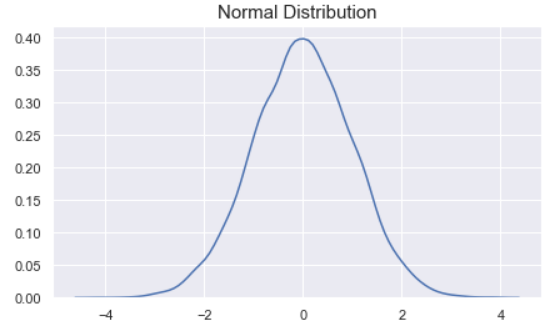
The peak of the curve indicates the most likely value the variable can take. As we move away from the peak the probability of the values decrease.

3. Measures of central tendency

Central tendency is the central (or typical) value of a probability distribution. The most common measures of central tendency are mean, median, and mode.

• Mean is the average of the values in series.
• Median is the value in the middle when values are sorted in ascending or descending order.
• Mode is the value that appears most often.

4. Variance and standard deviation

Variance is a measure of the variation among values. It is calculated by adding up squared differences of each value and the mean and then dividing the sum by the number of samples.

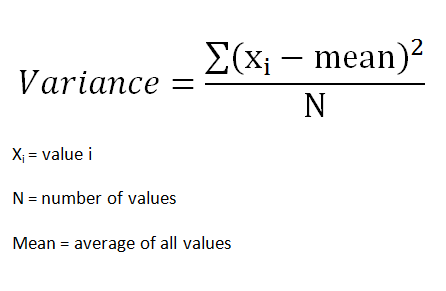
Standard deviation is a measure of how spread out the values are. To be more specific, it is the square root of variance.

Note: Mean, median, mode, variance, and standard deviation are basic descriptive statistics that help to explain a variable.

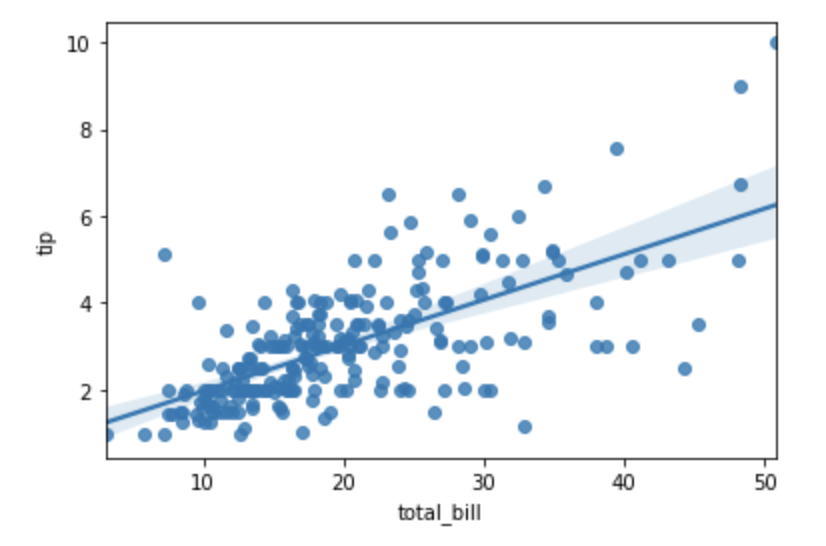
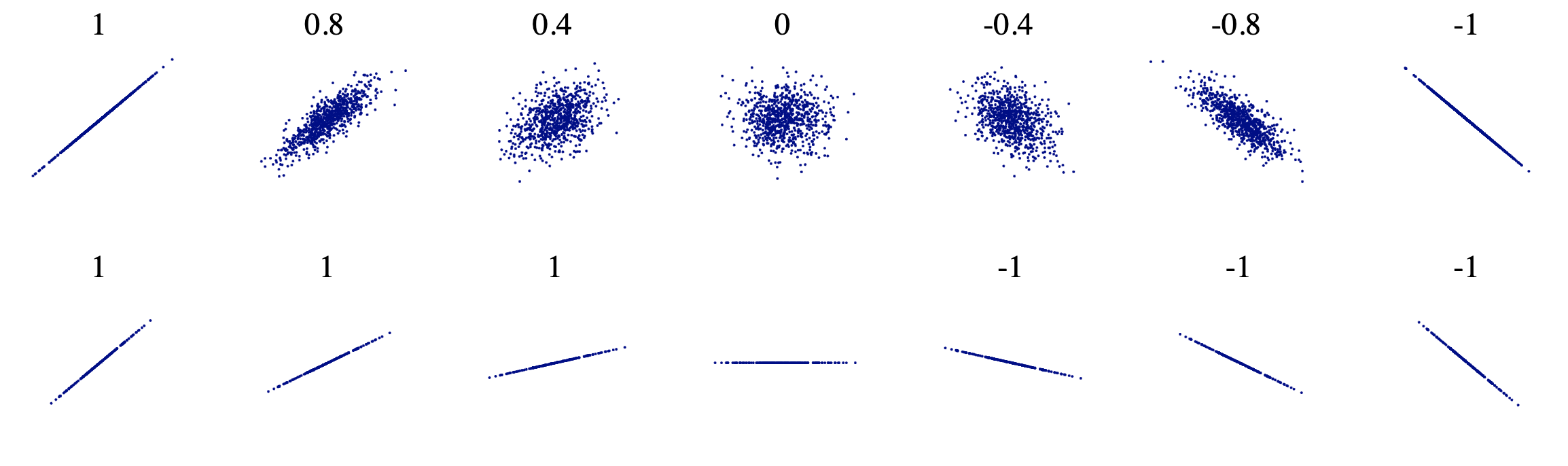
5. Covariance and correlation

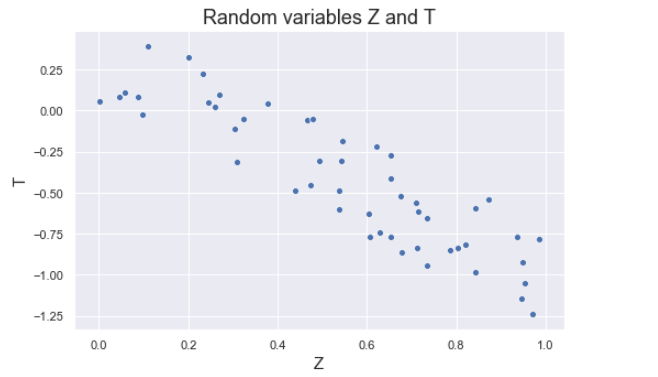
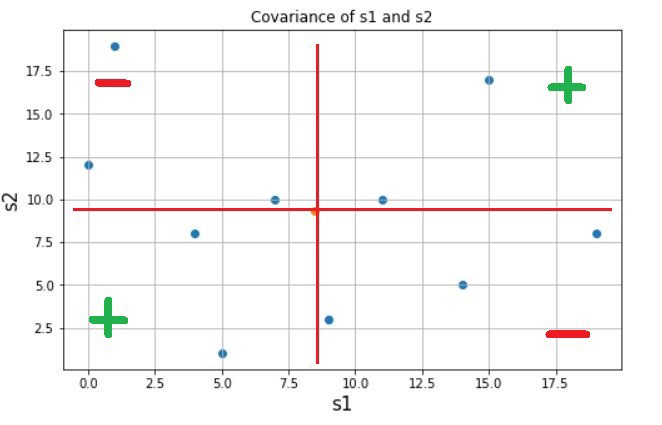
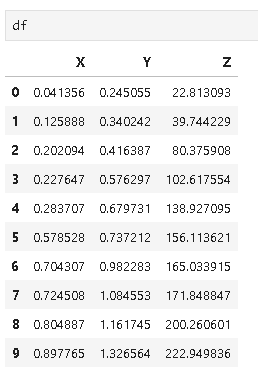
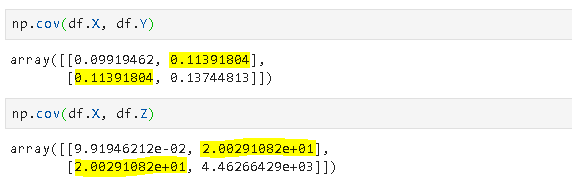
Covariance is a quantitative measure that represents how much the variations of two variables match each other. To be more specific, covariance compares two variables in terms of the deviations from their mean (or expected) value.

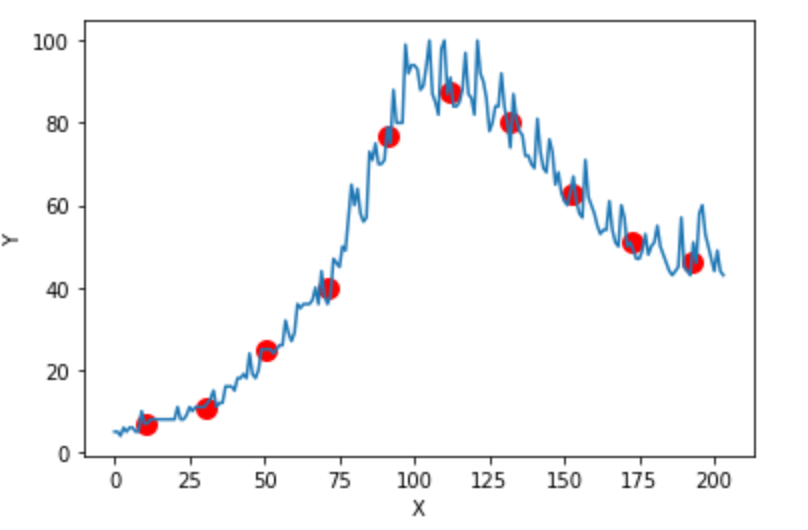
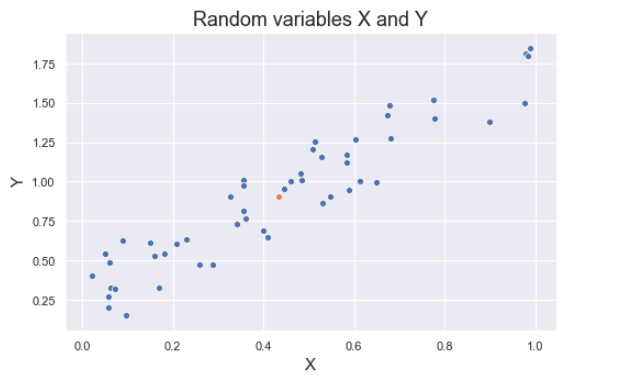
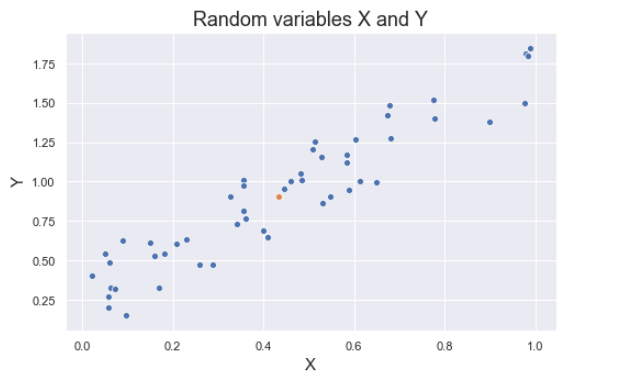
The figure below shows some values of the random variables X and Y. The orange dot represents the mean of these variables. The values change similarly with respect to the mean value of the variables. Thus, there is positive covariance between X and Y.

The formula for covariance of two random variables:

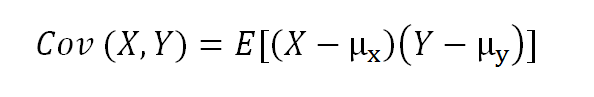
where E is the expected value and µ is the mean.

Note: The covariance of a variable with itself is the variance of that variable.

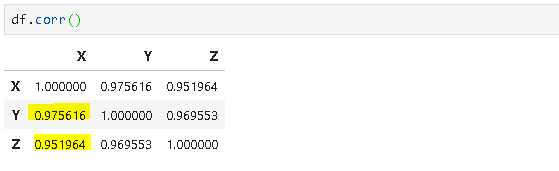
Correlation is a normalization of covariance by the standard deviation of each variable.

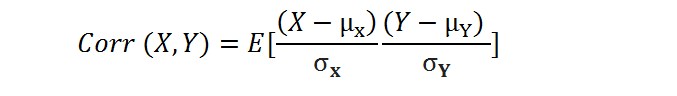
where σ is the standard deviation.

This normalization cancels out the units and the correlation value is always between 0 and 1. Please note that this is the absolute value. In case of a negative correlation between two variables, the correlation is between 0 and -1. If we are comparing the relationship among three or more variables, it is better to use correlation because the value ranges or unit may cause false assumptions.

6. Central limit theorem

In many fields including natural and social sciences, when the distribution of a random variable is unknown, normal distribution is used.

Central limit theorem (CLT) justifies why normal distribution can be used in such cases. According to the CLT, as we take more samples from a distribution, the sample averages will tend towards a normal distribution regardless of the population distribution.

Consider a case that we need to learn the distribution of the heights of all 20-year-old people in a country. It is almost impossible and, of course not practical, to collect this data. So, we take samples of 20-year-old people across the country and calculate the average height of the people in samples. CLT states that as we take more samples from the population, sampling distribution will get close to a normal distribution.

Why is it so important to have a normal distribution? Normal distribution is described in terms of mean and standard deviation which can easily be calculated. And, if we know the mean and standard deviation of a normal distribution, we can compute pretty much everything about it.

7. P-value

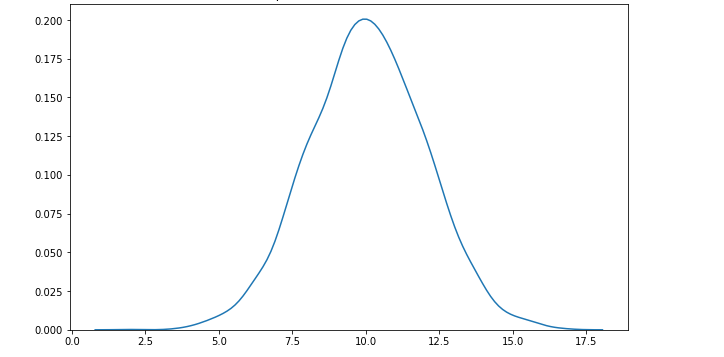
P-value is a measure of the likelihood of a value that a random variable takes. Consider we have a random variable A and the value x. The p-value of x is the probability that A takes the value x or any value that has the same or less chance to be observed. The figure below shows the probability distribution of A. It is highly likely to observe a value around 10. As the values get higher or lower, the probabilities decrease.

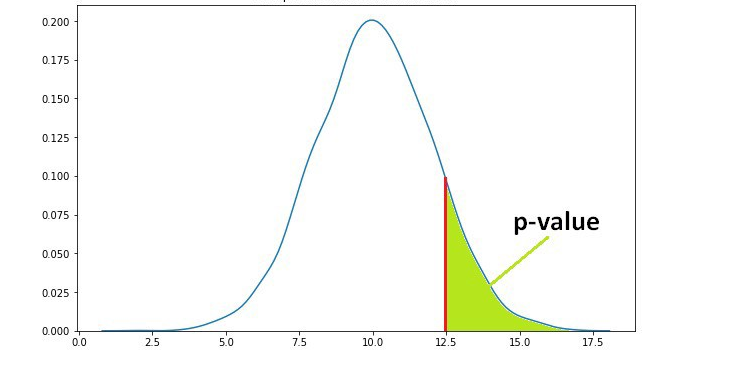
We have another random variable B and want to see if B is greater than A. The average sample means obtained from B is 12.5 . The p value for 12.5 is the green area in the graph below. The green area indicates the probability of getting 12.5 or a more extreme value (higher than 12.5 in our case).

Let’s say the p value is 0.11 but how do we interpret it? A p value of 0.11 means that we are 89% sure of the results. In other words, there is 11% chance that the results are due to random chance. Similarly, a p value of 0.05 means that there is 5% chance that the results are due to random chance.

Note: Lower p values show more certainty in the result.

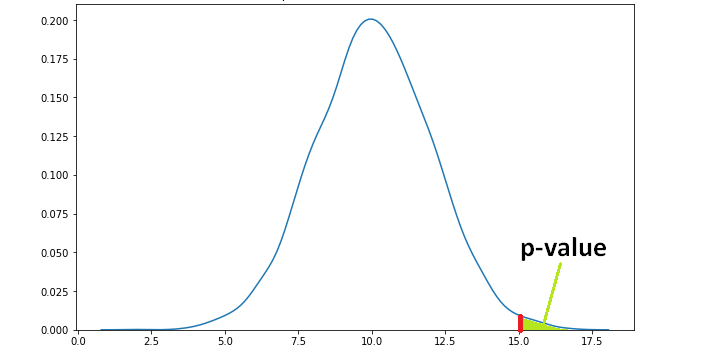
If the average of sample means from the random variable B turns out to be 15 which is a more extreme value, the p value will be lower than 0.11.

8. Expected value of random variables

The expected value of a random variable is the weighted average of all possible values of the variable. The weight here means the probability of the random variable taking a specific value.

The expected value is calculated differently for discrete and continuous random variables.

• Discrete random variables take finitely many or countably infinitely many values. The number of rainy days in a year is a discrete random variable.
• Continuous random variables take uncountably infinitely many values. For instance, the time it takes from your home to the office is a continuous random variable. Depending on how you measure it (minutes, seconds, nanoseconds, and so on), it takes uncountably infinitely many values.

The formula for the expected value of a discrete random variable is:

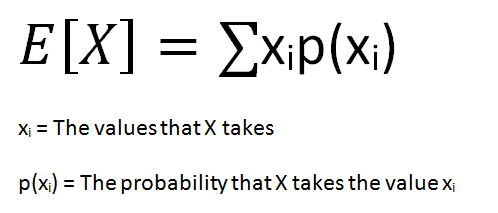
The expected value of a continuous random variable is calculated with the same logic but using different methods. Since continuous random variables can take uncountably infinitely many values, we cannot talk about a variable taking a specific value. We rather focus on value ranges.

In order to calculate the probability of value ranges, probability density functions (PDF) are used. PDF is a function that specifies the probability of a random variable taking value within a particular range.

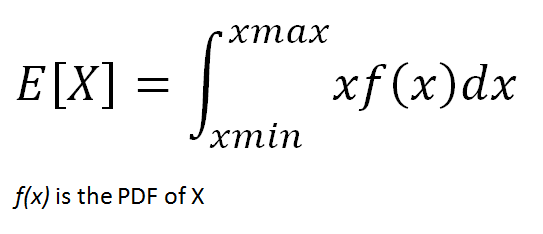
9. Conditional probability

Probability simply means the likelihood of an event to occur and always takes a value between 0 and 1 (0 and 1 inclusive). The probability of event A is denoted as p(A) and calculated as the number of the desired outcome divided by the number of all outcomes. For example, when you roll a die, the probability of getting a number less than three is 2 / 6. The number of desired outcomes is 2 (1 and 2); the number of total outcomes is 6.

Conditional probability is the likelihood of an event A to occur given that another event that has a relation with event A has already occurred.

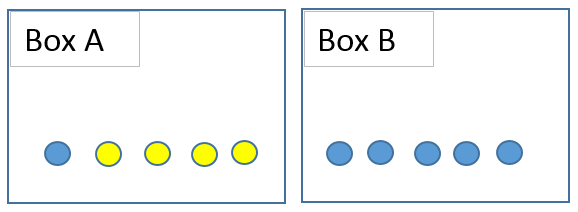
Suppose that we have 6 blue balls and 4 yellows placed in two boxes as seen below. I ask you to randomly pick a ball. The probability of getting a blue ball is 6 / 10 = 0,6. What if I ask you to pick a ball from box A? The probability of picking a blue ball clearly decreases. The condition here is to pick from box A which clearly changes the probability of the event (picking a blue ball). The probability of event A given that event B has occurred is denoted as p(A|B).

10. Bayes’ theorem

According to Bayes’ theorem, probability of event A given that event B has already occurred can be calculated using the probabilities of event A and event B and probability of event B given that A has already occurred.

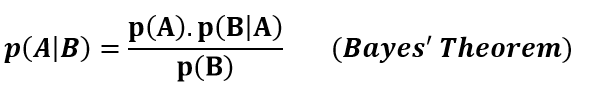
Bayes’ theorem is so fundamental and ubiquitous that a field called “bayesian statistics” exists. In bayesian statistics, the probability of an event or hypothesis as evidence comes into play. Therefore, prior probabilities and posterior probabilities differ depending on the evidence.

Naive bayes algorithm is structured by combining bayes’ theorem and some naive assumptions. Naive bayes algorithm assumes that features are independent of each other and there is no correlation between features.

Conclusion

We have covered some basic yet fundamental statistical concepts. If you are working or plan to work in the field of data science, you are likely to encounter these concepts.

There is, of course, much more to learn about statistics. Once you understand the basics, you can steadily build your way up to advanced topics.

Data binning (or bucketing) groups data in bins (or buckets), in the sense that it replaces values contained into a small interval with a single representative value for that interval. Sometimes binning improves accuracy in predictive models.

Data binning is a type of data preprocessing, a mechanism which includes also dealing with check this link missing values, formatting, normalization and standardization.

There are two approaches to perform data binning:

• numeric to categorical, which converts numeric into categorical variables
• sampling, wihch corresponds to data quantization.

You can download the full code of this tutorial from Github repository

Data Import

In this tutorial we exploit the cupcake.csv dataset, which contains the trend search of the word cupcake on Google Trends. Data are extracted from this link. We exploit the pandas library to import the dataset and we transform it into a dataframe through the read_csv() function.

import pandas as pd
df = pd.read_csv('cupcake.csv')
df.head(5)

Numeric to categorical binning

In this case we group values related to the column Cupcake into three groups: small, medium and big. In order to do it, we need to calculate the intervals within each group falls. We calculate the interval range as the difference between the maximum and minimum value and then we split this interval into three parts, one for each group. We exploit the functions min() and max() of dataframe to calculate the minimum value and the maximum value of the column Cupcake.

min_value = df['Cupcake'].min()
max_value = df['Cupcake'].max()
print(min_value)
print(max_value)

which gives the following output

4
100

Now we can calculate the range of each interval, i.e. the minimum and maximum value of each interval. Since we have 3 groups, we need 4 edges of intervals (bins):

• small — (edge1, edge2)
• medium — (edge2, edge3)
• big — (edge3, edge4) We can use the linspace() function of the numpy package to calculate the 4 bins, equally distributed.

import numpy as np
bins = np.linspace(min_value,max_value,4)
bins

which gives the following output:

array([  4.,  36.,  68., 100.])

Now we define the labels:

labels = ['small', 'medium', 'big']

We can use the cut() function to convert the numeric values of the column Cupcake into the categorical values. We need to specify the bins and the labels. In addition, we set the parameter include_lowest to True in order to include also the minimum value.

df['bins'] = pd.cut(df['Cupcake'], bins=bins, labels=labels, include_lowest=True)

We can plot the distribution of values, by using the hist() function of the matplotlib package.

import matplotlib.pyplot as pltplt.hist(df['bins'], bins=3)

Sampling

Sampling is another technique of data binning. It permits to reduce the number of samples, by grouping similar values or contiguous values. There are three approaches to perform sampling:

• by bin means: each value in a bin is replaced by the mean value of the bin.
• by bin median: each bin value is replaced by its bin median value.
• by bin boundary: each bin value is replaced by the closest boundary value, i.e. maximum or minimum value of the bin.

In order to perform sampling, the binned_statistic() function of the scipy.stats package can be used. This function receives two arrays as input, x_data and y_data, as well as the statistics to be used (e.g. median or mean) and the number of bins to be created. The function returns the values of the bins as well as the edges of each bin. We can calculate the x values (x_bins) corresponding to the binned values (y_bins) as the values at the center of the bin range.

from scipy.stats import binned_statistic
x_data = np.arange(0, len(df))
y_data = df['Cupcake']
y_bins,bin_edges, misc = binned_statistic(x_data,y_data, statistic="median", bins=10)
x_bins = (bin_edges[:-1]+bin_edges[1:])/2
x_bins

which gives the following output:

array([ 10.15,  30.45,  50.75,  71.05,  91.35, 111.65, 131.95, 152.25, 172.55, 192.85])

Finally, we plot results.

plt.plot(x_data,y_data)
plt.xlabel("X"); 
plt.ylabel("Y")plt.scatter(x_bins, y_bins,  color= 'red',linewidth=5)
plt.show()

Summary

In this tutorial I have illustrated how to perform data binning, which is a technique for data preprocessing. Two approaches can be followed. The first approach converts numeric data into categorical data, the second approach performs data sampling, by reducing the number of samples.

Data binning is very useful when discretization is needed.

This is the second part in Machine Learning series where we discuss on Features handling before using the data for machine learning models. The articles contains below parts:

1. Feature representation
2. Feature selection
3. Feature transformation
4. Feature engineering

This article cover the basic concepts of modifying the features as data needs to be refined before it can be used for prediction. We need to remove garbage out of data and turn features into high quality features.

Feature Representation

Your features need be represented as quantitative (preferably numeric) attributes of the thing you’re sampling. They can be real world values, such as the readings from a sensor, and other discernible, physical properties. Alternatively, your features can also be calculated derivatives, such as the presence of certain edges and curves in an image, or lack thereof.

But there is no guarantee that will be the case, and you will often encounter data in textual or other unstructured forms. Luckily, there are a few techniques that when applied, clean up these scenarios.

Textual Categorical-Features

If you have a categorical feature, the way to represent it in your dataset depends on if it’s ordinal or nominal. For ordinal features, map the order as increasing integers in a single numeric feature.

On the other hand, if your feature is nominal (and thus there is no obvious numeric ordering), then you have two options. The first is you can encoded it similar as you did above. This would be a fast-and-dirty approach. This may or may not cause problems for you in the future. If you aren’t getting the results you hoped for, or even if you are getting the results you desired but would like to further increase the result accuracy, then a more precise encoding approach would be to separate the distinct values out into individual boolean features:

These newly created features are called boolean features because the only values they can contain are either 0 for non-inclusion, or 1 for inclusion. Pandas .get_dummies() method allows you to completely replace a single, nominal feature with multiple boolean indicator features. This method is quite powerful and has many configurable options, including the ability to return a SparseDataFrame, and other prefixing options. It’s benefit is that no erroneous ordering is introduced into your dataset.

Pure Textual Features

If you are trying to “featurize” a body of text such as a webpage, a tweet, a passage from a newspaper, an entire book, or a PDF document, creating a corpus of words and counting their frequency is an extremely powerful encoding tool. This is also known as the Bag of Words model, implemented with the CountVectorizer() method in SciKit-Learn.

Graphical Features

In addition to text and natural language processing, bag of words has successfully been applied to images by categorizing a collection of regions and describing only their appearance, ignoring any spatial structure. However this is not the typical approach used to represent images as features, and requires you come up with methods of categorizing image regions. More often used methods include:

1. Split the image into a grid of smaller areas, and attempt feature extraction at each locality. Return a combined array of all discovered. features
2. Use variable-length gradients and other transformations as the features, such as regions of high / low luminosity, histogram counts for horizontal and vertical black pixels, stroke and edge detection, etc.
3. Resize the picture to a fixed size, convert it to grayscale, then encode every pixel as an element in a uni-dimensional feature array.

If you’re wondering what the :: is doing, that is called extended slicing. Notice the .reshape(-1) line. This tells Pandas to take your 2D image and flatten it into a 1D array. This is an all purpose method you can use to change the shape of your dataframes, so long as you maintain the number of elements. For example reshaping a [10, 10] to [100, 1] or [4, 25], etc. Another method called .ravel() will do the same thing as .reshape(-1), that is unravel a multi-dimensional NDArray into a one dimensional one. The reason why its important to reshape your 2D array images into one dimensional ones is because each image will represent a single sample, and Sklearn expects your dataframe to be shapes [num_samples, num_features].

Feature Selection

Most of the times, we will have many non-informative features. For Example, Name or ID variables and it results in “garbage-in, garbage-out”. Also, extra features make a model complex, time-consuming, and harder to implement in production. Many machine learning algorithms suffer from the curse of dimensionality — that is, they do not perform well when given a large number of variables or features. So it’s better to remove highly irrelevant or redundant features to simplify the situation and improve performance.

For instance, if your dataset have columns you don’t need, you can remove them using drop() method by specifying the name of columns. Axis=1 tells that deletion will happen column-wise while axis=0 will imply that deletion will happen row-wise.

Or, if you want only select columns for analysis or visualization purposes, you can select those columns by enclosing them within double square brackets.

Sometimes, we want to remove a feature but use it as an index instead. We can do this by specifying the column name as index during data load method.

We can set the column as index later as well by using set_index() method.

We can further improve the situation of having too many features through dimensionality reduction.

Commonly used techniques are:

• PCA (Principal Component Analysis) — Considered a more statistical approach than machine learning approach. It tries to preserve the essential parts that have more variation of the data and remove the non-essential parts with fewer variation. One important thing to note that it is an unsupervised dimensionality reduction technique, where you can cluster the similar data points based on the correlation between them without any labels.
• t-SNE (t-Distributed Stochastic Neighboring Entities) — In this approach, target number of dimensions is typically 2 or 3 which means that t-SNE is used a lot for visualizing your data as visualizing data with more than 3 dimensions is not easy for human brain. t-SNE has remarkable capability of keeping close points from multi-dimensional space close in the two-dimensional space.
• Feature embedding — It is based on training a separate machine learning model to encode a large number of features into small number of features

Feature Transformation

Pandas will automatically attempt to figure out the best data type to use for each series in your dataset. Most of the time it does this flawlessly, but other times it fails horribly! Particularly the .read_html() method is notorious for defaulting all series data types to Python objects. You should check, and double-check the actual type of each column in your dataset to avoid unwanted surprises. If your data types don’t look the way you expected them, explicitly convert them to the desired type using the .to_datetime(), .to_numeric(), and .to_timedelta() methods:

Take note how to_numeric properly converts to decimal or integer depending on the data it finds. The errors=’coerce’ parameter instructs Pandas to enter a NaN at any field where the conversion fails.

Sometimes, even though the data type is correct, but we still need to modify the values in features. Example — we need to divide all the values by 10 or we need to convert them to their logarithmic values.

Feature Engineering

Just as oil needs to be refined before it is used, similarly data needs to be refined before we use it for machine learning. Sometimes, we need to derive new features out of existing features. The process of extracting new features from existing ones is called feature engineering. Classical Machine Learning depends on feature engineering much more than Deep Learning.

Below are some types of Feature Engineering.

1. Aggregation — New features are created by getting a count, sum, average, mean, or median from a group of entities.
2. Part-Of — New features are created by extracting a part of data-structure. E.g. Extracting the month from a date.
3. Binning — Here you group your entities into bins and then you apply those aggregations over those bins. Example — group customers by age and then calculating average purchases within each group
4. Flagging—Here you derive a boolean (0/1 or True/False) value for each entity

Example — we need to summarize data by finding its sum, average, minimum or maximum value and then creating new features with those new values.

Detailed explanation with examples

Covariance and correlation are widely-used measures in the field of statistics, and thus both are very important concepts in data science. Covariance and correlation provide insight about the ralationship between random variables or features in a dataset. Although these two concepts are highly related, we need to interpret them carefully not to cause any misunderstandings.

Covariance

Covariance is a quantitative measure that represents how much the variations of two variables match each other. To be more specific, covariance compares two variables in terms of the deviations from their mean (or expected) value. Consider the random variables “X” and “Y”. Some realizations of these variables are shown in the figure below. The orange dot show the mean of X and mean of Y. As the values of a get away from the mean of X in positive direction, the values of Y tend to change in similar way. Same relation is valid for negative direction as well.

The formula for covariance of two random variables:

where E means the expectation and µ is the mean.

If X and Y change in the same direction, as in the figure above, covariance is positive. Let’s confirm with the covariance function of numpy:

np.cov() returns the covariance matrix. The covariance of X and Y is 0.11. The value at position [0,0] shows the covariance of X with itself and the value at [1,1] shows the covariance of Y with itself. If you run the code np.cov(X,X), you will get the value at position [0,0] which is 0.07707877 in this case. Similarly, np.cov(Y,Y) will return the value at position [1,1].

The covariance of a variable with itself is actually indicates the variance of that variable:

Let’s go over another example. The figure below shows some realizations of random variables Z and T. As we can see, as T increases, Z tends to decrease. Thus, the covariance of Z and T should be negative:

We may also see variables that the variations are independent of each other. For example, in the figure below, realizations of variables A and B seems changing randomly with respect to each other. In this case, we expect to see a covariance value that is close to zero. Let’s confirm:

The following example will provide a little more intuition about the calculation of covariance.

Covariance describes how similarly two random variables deviate from their mean. The red lines show the means of series. The mean of s1 is the vertical line (x=8.5) and the mean of s2 is the horizontol line (y=9.3). Deviation from the mean is the difference between the values and the mean. Covariance is proportional to the product of deviation of s1 and s2 values. Consider the upper right rectangle in the plot above. Both s1 and s2 values are higher than the mean of s1 and s2, respectively. So, deviations are positive. When we multiply two positive values, we get a positive value. In the lower left rectangle, s1 and s2 values are lower than the mean of s1 and s2, respectively. Thus, deviations are negative but we get a positive number when two negative numbers are multiplied. For the points in lower right and upper left rectangle areas, deviations of s1 is positive when the deviation of s2 is negative and vice versa. So we get a negative number when two deviations are multiplied. All the deviations are combined to get the covariance. Hence, if we have more points in negative regions than positive regions, we will get a negative covariance.

Correlation

Correlation is a normalization of covariance by the standard deviation of each variable.

where σ is the standard deviation.

This normalization cancels out the units and the correlation value is always between 0 and 1. Please note that this is the absolute value. In case of a negative correlation between two variables, the correlation is between 0 and -1. If we are comparing the relationship among three or more variables, it is better to use correlation because the value ranges or unit may cause false assumptions.

Consider the dataframe below:

We want to measure the relationship between X-Y and X-Z. We want to find out which variable (Y or Z) is more correlated with X. Let’s use covariance first:

Covariance of X and Z is much higher than the covariance of X and Y. We may think the relationship between the deviations in X and Z is much stronger than that of X and Y. However, it is not the case. Covariance of X and Z is higher because of the value ranges. The range of Z values are in between 22 and 222 whereas the values of Y are around 1 (most of them are less than 1). Therefore, we need to use correlation to eliminate the effect of different value ranges.

As we can see from the correlation matrix, X and Y are actually more correlated than X and Z.

Learn how to present the relationships amongst the features using multivariate charts and plots in Python

While dealing with a big dataset, it is important to understand the relationship between the features. That is a big part of data analysis. The relationships can be between two variables or amongst several variables. I will discuss how to present the relationships between multiple variables with some simple techniques. Python’s Numpy, Pandas, Matplotlib, and Seaborn libraries will be used.

First, import the necessary packages and the dataset to be used.

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
df = pd.read_csv("nhanes_2015_2016.csv")

This dataset is very large. At least too large to show a screenshot here. Here are the columns in this dataset.

df.columns
#Output:
Index(['SEQN', 'ALQ101', 'ALQ110', 'ALQ130', 'SMQ020', 'RIAGENDR', 'RIDAGEYR',        'RIDRETH1', 'DMDCITZN', 'DMDEDUC2', 'DMDMARTL', 'DMDHHSIZ', 'WTINT2YR',        'SDMVPSU', 'SDMVSTRA', 'INDFMPIR', 'BPXSY1', 'BPXDI1', 'BPXSY2',        'BPXDI2', 'BMXWT', 'BMXHT', 'BMXBMI', 'BMXLEG', 'BMXARML', 'BMXARMC',        'BMXWAIST', 'HIQ210'],       dtype='object')

Now, let’s make the dataset smaller with a few columns. So, it’s easier to handle and show in this article.

df = df[['SMQ020', 'RIAGENDR', 'RIDAGEYR','DMDCITZN', 
         'DMDEDUC2', 'DMDMARTL', 'DMDHHSIZ','SDMVPSU', 
         'BPXSY1', 'BPXDI1', 'BPXSY2', 'BPXDI2', 'RIDRETH1']]
df.head()

Column names may look strange to you. I will keep explaining as we keep using them.

1. In this dataset, we have two systolic blood pressure data (‘BPXSY1’, ‘BPXSY2) and two diastolic blood pressure data (‘BPXDI1’, ‘BPXDI2’). It is worth looking at if there is any relationship between them. Observe the relationship between the first and second systolic blood pressure.

To find out the relation between two variables, scatter plots have been being used for a long time. It is the most popular, basic, and easily understandable way of looking at a relationship between two variables.

sns.regplot(x = "BPXSY1", y="BPXSY2", data=df, fit_reg = False, scatter_kws={"alpha": 0.2})

The relationship between the two systolic blood pressures is positively linear. There is a lot of overlapping observed in the plot.

2. To understand the systolic and diastolic blood pressure data and their relationships more, make a joint plot. Jointplot shows the density of the data and the distribution of both the variables at the same time.

sns.jointplot(x = "BPXSY1", y="BPXSY2", data=df, kind = 'kde')

In this plot, it shows very clearly that the densest area is from 115 to 135. Both the first and second systolic blood pressure distribution is right-skewed. Also, both of them have some outliers.

3. Find out if the correlation between the first and second systolic blood pressures are different in the male and female population.

df["RIAGENDRx"] = df.RIAGENDR.replace({1: "Male", 2: "Female"}) 
sns.FacetGrid(df, col = "RIAGENDRx").map(plt.scatter, "BPXSY1", "BPXSY2", alpha =0.6).add_legend()

This picture shows, both the correlations are positively linear. Let’s find out the correlation with more clarity.

print(df.loc[df.RIAGENDRx=="Female",["BPXSY1", "BPXSY2"]].dropna().corr())
print(df.loc[df.RIAGENDRx=="Male",["BPXSY1", "BPXSY2"]].dropna().corr())

From the two correlation chart above, the correlation between two systolic blood pressure is 1% higher in the female population than in the male. If these things are new to you, I encourage you to try understanding the correlation between two diastolic blood pressures or systolic and diastolic blood pressures.

4. Human behavior can change with so many different factors such as gender, education level, ethnicity, financial situation, and so on. In this dataset, we have ethnicity (“RIDRETH1”) information as well. Check the effect of both ethnicity and gender on the relationship between both the systolic blood pressures.

sns.FacetGrid(df, col="RIDRETH1", row="RIAGENDRx").map(plt.scatter, "BPXSY1", "BPXSY2", alpha = 0.5).add_legend()

With different ethnic origins and gender, correlations seem to be changing a little bit but generally stays positively linear as before.

5. Now, focus on some other variables in the dataset. Find the relationship between education and marital status.

Both the education column(‘DMDEDUC2’) and the marital status (‘DMDMARTL’) column are categorical. First, replace the numerical values with the string values that will make sense. We also need to get rid of values that do not add good information to the chart. Such as the education column has some values ‘Don’t know’ and the marital status column has some ‘Refused’ values.

df["DMDEDUC2x"] = df.DMDEDUC2.replace({1: "<9", 2: "9-11", 3: "HS/GED", 4: "Some college/AA", 5: "College", 7: "Refused", 9: "Don't know"})df["DMDMARTLx"] = df.DMDMARTL.replace({1: "Married", 2: "Widowed", 3: "Divorced", 4: "Separated", 5: "Never married", 6: "Living w/partner", 77: "Refused"})db = df.loc[(df.DMDEDUC2x != "Don't know") & (df.DMDMARTLx != "Refused"), :]

Finally, we got this DataFrame that is clean and ready for the chart.

x = pd.crosstab(db.DMDEDUC2x, db.DMDMARTLx)
x

Here is the result. The numbers look very simple to understand. But a chart of population proportions will be a more appropriate presentation. I am getting a population proportion based on marital status.

x.apply(lambda z: z/z.sum(), axis=1)

6. Find the population proportion of marital status segregated by Ethnicity (‘RIDRETH1’) and education level.

First, replace the numeric value with meaningful strings in the ethnicity column. I found these string values from the Center for Disease Control website.

db.groupby(["RIDRETH1x", "DMDEDUC2x", "DMDMARTLx"]).size().unstack().fillna(0).apply(lambda x: x/x.sum(), axis=1)

7. Observe the difference in education level with age.

Here, education level is a categorical variable and age is a continuous variable. A good way of observing the difference in education levels with age will be to make a boxplot.

plt.figure(figsize=(12, 4))
a = sns.boxplot(db.DMDEDUC2x, db.RIDAGEYR)

This plot shows, the rate of a college education is higher in younger people. A violin plot may provide a better picture.

plt.figure(figsize=(12, 4))
a = sns.violinplot(db.DMDEDUC2x, db.RIDAGEYR)

So, the violin plot shows a distribution. The most college-educated people are around age 30. At the same time, most people who are less than 9th grade, are about 68 to 88 years old.

8. Show the marital status distributed by and segregated by gender.

fig, ax = plt.subplots(figsize = (12,4))
ax = sns.violinplot(x= "DMDMARTLx", y="RIDAGEYR", hue="RIAGENDRx", data= db, scale="count", split=True, ax=ax)

Here, blue color shows the male population distribution and orange color represents the female population distribution. Only ‘never married’ and ‘living with partner’categories have similar distributions for the male and female populations. Every other category has a notable difference in the male and female populations.

Introducing the exploretransform package for Python

Summary:

• Data scientists spend 60% of their time on cleaning and organizing data. Collecting data sets comes second at 19% of their time, meaning data scientists spend around 80% of their time on preparing and managing data for analysis¹
• 76% of data scientists view data preparation as the least enjoyable part of their work²

In this article, I will be demonstrating Python’s exploretransform package. It can save time during data exploration and transformation and hopefully make your data preparation more enjoyable!

Overview:

I originally developed exploretransform for use in my own projects, but I figured it might be useful for others. My intention was to create a simple set of functions and classes that returned results in common Python data formats. This would enable practitioners to easily utilize the outputs or extend the original functions as part of their workflows.

How to use exploretransform:

Installation and import

!pip install exploretransformimport exploretransform as et

Let’s start by loading the Boston corrected dataset.

df, X, y = et.loadboston()

At this stage, I like to check that the data types align with the data dictionary and first five observations. Also, the # of lvls can indicate potential categorical features or features with high cardinality. Any dates or other data that need reformatting can also be detected here. We can use peek() here.

et.peek(X)

After analyzing the data types, we can use explore() to identify missing, zero, and infinity values.

et.explore(X)

Earlier, we saw that town was likely a categorical feature with high cardinality. We can use freq() to analyze categorical or ordinal features providing the count, percent, and cumulative percent for each level

t = et.freq(X['town'])t

To visualize the resutls of freq() we can use plotfreq(). It generates a bar plot showing the levels in descending order.

et.plotfreq(t)

To pair with histograms you probably normally examine, skewstats() returns the skewness statistics and magnitude for each numeric feature. When you have too many features to easily plot, this function becomes more useful.

et.skewstats(N)

In order to determine the association between the predictors and target, ascores() calculates pearson, kendall, pearson, spearman, mic, and dcor statistics. A variety of these scores is useful since certain scores measure linear associations and others will detect non-linear relationships.

et.ascores(N,y)

Correlation matrices can get unwieldy once we hit a certain number of features. While the Boston dataset is well below this threshold, one can imagine that having a table might be more useful than a matrix when dealing with high dimensionality. Corrtable() returns a table of all pairwise correlations and uses the average correlation for the row and column in to decide on potential drop/filter candidates. You can use any of the methods you normally would with pandas corr function:

• pearson
• kendall
• spearman
• callable

N = X.select_dtypes('number').copy()c = et.corrtable(N, cut = 0.5, full= True, methodx = 'pearson')c

Based on the output of corrtable(), calcdrop() determines which features should be dropped.

et.calcdrop(c)['age', 'indus', 'nox', 'dis', 'lstat', 'tax']

ColumnSelect() is a custom transformer that selects columns for pipelines

categorical_columns = ['rad', 'town']cs = et.ColumnSelect(categorical_columns).fit_transform(X)cs

CategoricalOtherLevel() is a custom transformer that creates “other” level in categorical / ordinal data based on threshold. This is useful in situation where you have high cardinality predictors and when there is a possibility of having new categories appear in future data.

co = et.CategoricalOtherLevel(colname = 'town', threshold = 0.015).fit_transform(cs)co.iloc[0:15, :]

CorrelationFilter() is a custom transformer that filters numeric features based on pairwise correlation. It uses corrtable() and calcdrop() to perform the drop evaluations and calcuations. For more information on how it works please see: Are you dropping too many correlated features?

cf = et.CorrelationFilter(cut = 0.5).fit_transform(N)cf

Conclusion:

In this article, I have demonstrated how the exploretransform package can help you accelerate your exploratory data analysis. 

Exploring the Unknown [Data]

This article is going to be about the first look every data enthusiast has taken into their project’s dataset. Before machine learning, before modeling, before feature selection — there has to be a fundamental understanding of the data you are using. That’s what we are doing — exploring. This article is about EDA, exploratory data analysis.

We will take it through several steps of analysis and even introduce a few techniques that help us determine the best course of action. For this article, I am going to assume you understand the difference between continuous and categorical data and knowledge about the different packages Python has to offer.

First, we are going to load a dataset that is relatively small and easy to understand. Luckily, Seaborn has a few datasets to choose from and I’ve decided to go with the ‘tips’ dataset and with it some other packages for this session like Matplotlib, Pandas, and SciPy. So the first step is to load it into a data frame in order to be used.https://medium.com/media/6c7e79e9b296e4dca7f88a5b12640557

Next, we look at a small portion of the data frame using the .head() method in order to understand the features that come along with the dataset.https://medium.com/media/6e7511a71b794ffb20564354ee9e1e61

And that gives us the output:

Now that we have looked at the dataset in order to make sure it loaded correctly and to get a feel of the features we can begin.

0. Looking at the Data Frame Shape

Before we look at the different features, I would suggest using .shape method. It returns a simple tuple that returns the dimensions of the data frame.https://medium.com/media/05ee5cda462a16d05a99436fa4ead569

The output for the tips data frame is:

While we are not going to necessarily need it for this data frame, you may run into data sets with hundreds of features and thousands of rows.

1. Descriptive Statistics

Python has a great method to use when you want an overview of a dataset. That is the .describe() method. Describe, when used on a data frame, allows us to see the statistical breakdown of the data frame. It is a great place to start and we can tailor it to the types of features we have. In this data frame, we have both continuous and categorical features. The statistical breakdown works differently on either one but you can use .describe() on both.https://medium.com/media/78142b25b9698dea407496876fa38d1a

The output for both at the same time is interesting, so let’s take a look.

The output from the code gives us insight into the statistics of the data frame. At the top of the breakdown is information about the data frame itself. The count is the number of observations (rows) that are in the data frame.

Before I go into the rest of the rows, I want to point out the NaN values. When you use the .describe() method on all of the features at once you apply all the statistics to all of them. This means that you will have statistics that aren’t applicable to one feature or another. For instance, the mean doesn’t make sense on a feature using days of the week. Mean is for numbers, the day of the week is a word. The same goes for unique — you can’t ask for the unique values of tips because there could be any number of different tip amounts.

Below that, are the statistics for categorical values. I am going to give a breakdown of the rest of the categorical statistics.

Remember, the list below will results in a NaN for continuous variables.

Categorical Statistics:

• Unique — how many different entries are in the variable.
• Top — the categorical answer that appears most frequently in the data frame
• Freq— the number of times the value that the most in a data frame

Next are the continuous variables and will result in a NaN for categorical variables.

Continuous Statistics:

• Mean — the average of all of the observations in that feature
• Std — the standard deviation of all of the variables in that feature
• Min — the lowest value out of all the observations
• 25% — this number is the location where the lowest quartile is
• 50% — this is the median of the feature
• 75% — this is where the upper quartile is
• Max — the largest value of the feature

I would recommend using the include=’all’ parameter when using the .describe() method. It saves time and is still very easy to understand.

2. Groupby

An expansion of the .describe() method use is using the .groupby() method.We can delve deeper into different features and use that information to make more informed decisions. Assume you want to know if there is any relationship between the different days a meal was eaten and the amount on the total bills.

An example of the .groupby() method below allows us to check the mean of the total bill and the size of the party based on the day the meal was taken.https://medium.com/media/f3195fd3e2aa18ea27eba0530f4e1966

When this code was run, it returned the following:

What is seen above is each day with the average value of the total bill and the size of the party. This can be done with any combination of continuous variables. More documentation on Pandas .groupby() can be found here.

A sidenote on the .groupby() method is the .value_counts() method. This returns the count for each unique entry. For instance, we apply it to the day categories in order to see how the days stack up against each other.https://medium.com/media/f0290504be63141f85c0b00369b46a49

The return is:

The default order is descending so the method returns the most frequently occurring day at the top. Notice the last line that has the information Name and type. This is simply referring to the name of the column that was counted and the type of information it returned in the picture above. Each of the counts returned is done so in the int64 format.

3. Correlation

Testing for correlation is the process of establishing a relationship or connection between two or more measures. Right now, we are going to look at whether an increase in the total bill results in an increase in the tip left for the server.

Our first test can be an easy graph where we look at a scatter plot of the independent variable total_bill vs the dependent variable tip.https://medium.com/media/9efc6fa1e5788d7c7c947a053b64bf58

And we get the plot:

From the plot, we can see there is some linear relationship between the two variables. However, just because two variables seem to increase at the same time doesn’t mean that we know to what degree they both change. For this analysis, we need a more refined method of seeking correlation using statistics.

4. Correlation Statistics

To understand the idea of correlation statistics on a fundamental level, we need to know about two concepts. The Pearson Coefficient and the P-Value. First, let’s talk about the Pearson Coefficient.

Pearson Coefficient

The Pearson Coefficient a statistic that measures the linear correlation between two variables a and b. It has a value between +1 and −1. A value of +1 is a total positive linear correlation, 0 is no linear correlation, and −1 is a total negative linear correlation.

As stated above, the correlation of +1 and -1 are very strong correlations, positively, and negatively respectively. A strong correlation does not indicate the slope of the line but rather only the tightness of fit to the sloped line.

P-Value

The p-value is a measure of the probability that an observed difference could have occurred just by random chance. The lower the p-value, the less likely the connection between the two variables happened randomly.

SciPy Statsmodel Package

Finally, we will use Python to determine the Pearson Coefficient and the p-value of the total bill’s impact on the change in the tip given. Working off of the Statsmodel library of the SciPy package, we use the pearsonr() function.https://medium.com/media/df5e69f39ba9d832d18f0734b97940d7Using the Pearson Correlation function from SciPy

The output from the code above is:

Analyzing our output we can come to two very important conclusions. Firstly, the Pearson coefficient is relatively high. With a value of 0.67, there is a relatively strong positive correlation between the total bill and the tips given.

Secondly, the p-value is very small. So small, in fact, that we can reject the idea that the correlation between the two variables is insignificant.

Conclusion

To summarize what we’ve learned today:

• It is important to get a feel for the dimensions of a data frame before beginning to work with it.
• Usage of the .describe() method to examine the continuous and categorical variables
• We use .groupby() to see how specific attributes stack up in terms of aggregate functions
• Correlation is the idea that two variables change at the same time.
• Pearson Coefficient determines the correlation value. +1 is a strong positive correlation, -1 is a strong negative correlation. 0 is no correlation.
• The p-value dictates how likely something is to occur. A large p-value means that a thing occurring happened by chance. A very small p-value means that a thing occurred not by chance, but because it has a good chance of being statistically significant.

I hope this guide helped you with the beginnings of your data science project.

Investigating Population, Gender Equality in Education & Income for Singapore, United States and China

Exploratory Data Analysis (EDA) is one of the most important aspect in every data science or data analysis problem. It provides us greater understanding on our data and can possibly unravel hidden insights that aren’t that obvious to us. This post will focus more on graphical EDA in Python using matplotlib, regression line and even motion chart!

Dataset

The dataset we are using for this article can be obtained from Gapminder, and drilling down into Population, Gender Equality in Education and Income.

The Population data contains yearly data regarding the estimated resident population, grouped by countries around the world between 1800 and 2018.

The Gender Equality in Education data contains yearly data between 1970 and 2015 on the ratio between female to male in schools, among 25 to 34 years old which includes primary, secondary and tertiary education across different countries

The Income data contains yearly data of income per person adjusted for differences in purchasing power (in international dollars) across different countries around the world, for the period between 1800 and 2018.

EDA on Population

Let’s first plot the population data over time, and focus mainly on the three countries Singapore, United States and China. We will use matplotlib library to plot 3 different line charts on the same figure.

import pandas as pd
import matplotlib.pylab as plt
%matplotlib inline# read in data
population = pd.read_csv('./population.csv')# plot for the 3 countries
plt.plot(population.Year,population.Singapore,label="Singapore")
plt.plot(population.Year,population.China,label="China")
plt.plot(population.Year,population["United States"],label="United States")# add legends, labels and title
plt.legend(loc='best')
plt.xlabel('Year')
plt.ylabel('Population')
plt.title('Population Growth over time')
plt.show()

As seen in the figure, the population values for the 3 countries Singapore, China and United States are increasing over time, though Singapore is not that visible since the axis is in billions, while the population in Singapore is only in the millions.

Now, let’s try to fit a linear regression line using linregressto the Singapore population data and plot the linear fit. We can even try predicting the Singapore population in 2020 and 2100.

from scipy.stats import linregress
# set up regression line
slope, intercept, r_value, p_value, std_err = linregress(population.Year,population.Singapore)
line = [slope*xi + intercept for xi in population.Year]# plot the regression line and the linear fit
plt.plot(population.Year,line,'r-', linewidth=3,label='Linear Regression Line')
plt.scatter(population.Year, population.Singapore,label='Population of Singapore')
plt.legend(loc='best')
plt.xlabel('Year')
plt.ylabel('Population')
plt.title('Population Growth of Singapore over time')
plt.show()# Calculate correlation coefficient to see how well is the linear fit
print("The correlation coefficient is " + str(r_value))
## Use the linear fit to predict the resident population in Singapore in 2020 and 2100.
# Using equation y=mx + c, i.e. population=slope*year + intercept
print("The predicted population in Singapore in 2020 will be " + str((slope*2020)+intercept))
print("The predicted population in Singapore in 2100 will be " + str((slope*2100)+intercept))

From the figure, we see that the linear fit did not seem to fit the Population of Singapore that well though we have a correlation coefficient close to 1. The prediction of the population was also well off as the current population of Singapore in 2020 is around 5.6 million, which is way above the 3.4 million predicted.

Notice that the population before 1850s were negative, which is definitely impossible. Since Singapore is founded in 1965, let’s filter to only use data from 1965 onwards.

from scipy.stats import linregress
# set up regression line
slope, intercept, r_value, p_value, std_err = linregress(population.Year[population.Year>=1965],population.Singapore[population.Year>=1965])
line = [slope*xi + intercept for xi in population.Year[population.Year>=1965]]plt.plot(population.Year[population.Year>=1965],line,'r-', linewidth=3,label='Linear Regression Line')
plt.scatter(population.Year[population.Year>=1965], population.Singapore[population.Year>=1965],label='Singapore')
plt.legend(loc='best')
plt.xlabel('Year')
plt.ylabel('Population')
plt.title('Population Growth of Singapore from 1965 onwards')
plt.show()# Calculate correlation coefficient to see how well is the linear fit
print("The correlation coefficient is " + str(r_value))
## Use the linear fit to predict the resident population in Singapore in 2020 and 2100.
# Using equation y=mx + c, i.e. population=slope*year + intercept
print("The predicted population in Singapore in 2020 will be " + str((slope*2020)+intercept))
print("The predicted population in Singapore in 2100 will be " + str((slope*2100)+intercept))

This linear regression line fits so much better as shown in the graph as well as the correlation coefficient. Furthermore, the predicted 2020 population is exactly what it is in Singapore currently, and let’s hope the 2100 population is not true since we know the land area in Singapore is considerably small.

EDA on Gender Equality in Education

Moving onto the second dataset, let’s try to plot the gender ratio (females to males) in schools for Singapore, China and the United States over time. We can also look at the maximum and minimum gender ratio percentage in Singapore.

# reading in data
gender_equality = pd.read_csv('./GenderEquality.csv')
# plot the graphs
plt.plot(gender_equality.Year,gender_equality.Singapore,label="Singapore")
plt.plot(gender_equality.Year,gender_equality.China,label="China")
plt.plot(gender_equality.Year,gender_equality["United States"],label="United States")# set up legends, labels and title
plt.legend(loc='best')
plt.xlabel('Year')
plt.ylabel('Gender Ratio of Female to Male in school')
plt.title('Gender Ratio of Female to Male in school over time')
plt.show()# What are the maximum and minimum values for gender ratio in Singapore over the time period?
print("The maximum value is: " + str(max(gender_equality.Singapore)) + " and the minimum is " 
      + str(min(gender_equality.Singapore)))

The gender ratios were generally increasing over time as seen in the output above. Gender Ratio for China and Singapore were increasing linearly over time. For United States, there was certain periods in which the gender ratio were stagnant before increasing again. The minimum gender ratio for Singapore was 79.5 while the maximum was 98.9, and this was expected since education in Singapore in the past was considerably more important for males than females.

Let’s plot the linear regression line on the gender ratio for Singapore.

# plot the regression line
slope, intercept, r_value, p_value, std_err = linregress(gender_equality.Year,gender_equality["Singapore"])
line = [slope*xi + intercept for xi in gender_equality.Year]plt.plot(gender_equality.Year,line,'r-', linewidth=3,label='Linear Regression Line')
plt.plot(gender_equality.Year, gender_equality["Singapore"],label='Singapore')
plt.legend(loc='best')
plt.xlabel('Year')
plt.ylabel('Gender Ratio of Female to Male in school')
plt.title('Gender Ratio of Female to Male in school for Singapore over time')
plt.show()
print("The correlation coefficient is " + str(r_value))

The correlation coefficient suggested that it is a good fit and gender ratio will potentially reach 100% in the future. This could be possible as education is no longer a privilege in Singapore as both males and females have equal opportunities in receiving formal education.

EDA on Income

Let’s finally move to Income data and plot the income of Singapore, United States and China over time.

# read in data
income = pd.read_csv('./Income.csv')
# plot the graphs
plt.plot(income.Year,income.Australia,label="Singapore")
plt.plot(income.Year,income.China,label="China")
plt.plot(income.Year,income["United States"],label="United States")
# set up legends, labels, title
plt.legend(loc='best')
plt.xlabel('Year')
plt.ylabel('Income per person')
plt.title('Income per person over time')
plt.show()

Surprisingly, the income per person in Singapore is comparable to the United States, with both above those in China.

Motion Chart — Visualising relationships over time

Now, let’s try to build a motion chart to visualise relationships over time for all three factors of Population, Gender Ratio and Income. In order to build a motion chart in Python, we will need motionchart library.

Before that, we will need to merge all three datasets into a single one to plot our motion chart easily. Merging can be done using common pandas commands.

# Convert columns into rows for each data set based on country and population/gender ratio/income
population=pd.melt(population,id_vars=['Year'],var_name='Country',value_name='Population')
gender_equality=pd.melt(gender_equality,id_vars=['Year'],var_name='Country',value_name='Gender Ratio')# Merge the 3 datasets into one on common year and country
income=pd.melt(income,id_vars=['Year'],var_name='Country',value_name='Income')
overall=pd.merge(population,gender_equality,how="inner",on=["Year","Country"])
overall=pd.merge(overall,income,how="inner",on=["Year","Country"])

To visualise relationship over time, we will need to set the Year attribute as the key in our motion chart. Our x-axis will be the Gender Ratio, y-axis the Income, size of the bubble for Population and lastly, colour of bubble for the Country.

from motionchart.motionchart import MotionChart# setting up the style
%%html
<style>
.output_wrapper, .output {
    height:auto !important;
    max-height:1000px; 
}
.output_scroll {
    box-shadow:none !important;
    webkit-box-shadow:none !important;
}
</style># plotting the motion chart
mChart = MotionChart(df = overall)
mChart = MotionChart(df = overall, key='Year', x='Gender Ratio', y='Income', xscale='linear'
                     , yscale='linear',size='Population', color='Country', category='Country')
mChart.to_notebook()

If we explore this motion chart, we know Afghanistan and Yemen had the lowest gender ratio in education of 23.7 and 30.1 respectively. Lesotho in South Africa has the highest gender ration throughout (note the little pink dot at the bottom right).

There is generally not a clear relationship between income and gender ratio in education. During the whole period of time, as gender ratio is generally increasing for all countries, income did not follow likewise by increasing nor did it decrease. There was a mix of being stagnant, increasing and decreasing which did not exhibit any clear relationship with gender ratio.

Let’s focus on building a motion chart for just Singapore.

mChart = MotionChart(df = overall.loc[overall.Country.isin(['Singapore'])])
mChart = MotionChart(df = overall.loc[overall.Country.isin(['Singapore'])], key='Year', x='Gender Ratio', 
y='Income', xscale='linear', yscale='linear',size='Population', color='Country', category='Country')
mChart.to_notebook()

Interestingly for Singapore, other than the Population increasing over time, Gender Ratio in Education as well as Income seems to increasing constantly over time as well. Income was at 11400 in 1970 and it increased tremendously to 80900 in 2015.

Summary

In this article, we made use of Python matplotlib, linear regression as well as the fanciful motion charts to conduct exploratory data analysis on three datasets, mainly Population, Gender Ratio in Education & Income. Through these graphical methods, we can discover some insights on our data and potentially, allow us to make better predictions. Hope you guys enjoy this graphical approach to Exploratory Data Analysis in Python, and have fun playing with your fanciful motion charts!

Why we should not use Pandas Alone

Handling missing values is an important data preprocessing step in machine learning pipelines.

Pandas is versatile in terms of detecting and handling missing values. However, when it comes to model training and evaluation with cross validation, there is a better approach.

The imputer of scikit-learn along with pipelines provide a more practical way of handling missing values in cross validation process..

In this post, we will first do a few examples that show different ways to handle missing values with Pandas. After that, I will explain why we need a different approach to handle missing values in cross validation.

Finally, we will do an example using the missing value imputer and pipeline of scikit-learn.

Let’s start with Pandas. Here is a simple dataframe with a few missing values.

import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randint(10, size=(8,5)), columns=list('ABCDE'))
df.iloc[[1,4],[0,3]] = np.nan
df.iloc[[3,7],[1,2,4]] = np.nan

df

The isna function returns Boolean values indicating the cells with missing values. The isna().sum() gives us the number of missing values in each column.

df.isna().sum()
A    2
B    2
C    2
D    2
E    2
dtype: int64

The fillna function is used to handle missing values. It provides many options to fill in. Let’s use a different method for each column.

df['A'].fillna(df['A'].mean(), inplace=True)
df['B'].fillna(df['B'].median(), inplace=True)
df['C'].fillna(df['C'].mode()[0], inplace=True)
df['D'].fillna(method='ffill', inplace=True)
df['E'].fillna(method='bfill', inplace=True)

The missing values in columns A, B, and C are filled with mean, median, and mode of the column, respectively. For column D, we used ‘ffill’ method which uses the previous value in the column to fill a missing value. The ‘bfill’ does the opposite.

Here is the updated version of the dataframe:

We still have one missing value in column D because we used the ‘bfill’ method for this column. With this method, the missing values are supposed to be filled with the values after them. Since the last value is a missing value, it was not changed.

The fillna function also accepts constant values. Let’s replace the last missing value with a constant.

df['E'].fillna(4, inplace=True)

As you have seen, the fillna function is pretty flexible. However, when it comes to train machine learning models, we need to be careful at handling the missing values.

Unless we use constant values, the missing values need to be handled after splitting the training and test sets. Otherwise, the model will be given information about the test set which causes data leakage.

Data leakage is a serious issue in machine learning. Machine learning models should not be given any information about the test set. The data points in the test sets need to be previously unseen.

If we use the mean of the entire data set to fill in missing values, we leak information about the test set to the model.

One solution is to handle missing values after train-test split. It is definitely an acceptable way. What if we want to do cross validation?

Cross validation means partitioning the data set into subsets (i.e. folds). Then, run many iterations with different combinations so that each example will be used in both training and testing.

Consider the case with 5-fold cross validation. The data set is divided into 5 subsets (i.e. folds). At each iteration, 4 folds are used in training and 1 fold is used in testing. After 5 iterations, each fold will be used in both training and testing.

We need a practical way to handle missing values in cross validation process in order to prevent data leakage.

One way is to create a Pipeline with scikit-learn. The pipeline accepts data preprocessing functions and can be used in the cross validation process.

Let’s create a new dataframe that fits a simple linear regression task.

df = pd.DataFrame(np.random.randint(10, size=(800,5)), columns=list('ABCDE'))
df['F'] = 2*df.A + 3*df.B - 1.8*df.C + 1.12*df.D - 0.5
df.iloc[np.random.randint(800, size=10),[0,3]] = np.nan
df.iloc[np.random.randint(800, size=10),[1,2,4]] = np.nan
df.head()

The columns A through E have 10 missing values. The column F is a linear combination of other columns with an additional bias.

Let’s import the required libraries for our task.

from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer

The SimpleImputer fills in missing values based on the given strategy. We can create a pipeline that contains a simple imputer object and a linear regression model.

imputer = SimpleImputer(strategy='mean')
regressor = Pipeline(
steps=[('imputer', imputer), ('regressor', LinearRegression())]
)

The “regression” pipeline contains a simple imputer that fills in the missing values with mean. The linear regression model does the prediction task.

We can now use this pipeline as estimator in cross validation.

X = df.drop('F', axis=1)
y = df['F']scores = cross_val_score(regressor, X, y, cv=4, scoring='r2')

scores.mean()
0.9873438657209939

The R-squared score is pretty high because this is a pre-designed data set.

The important point here is to handle missing values after splitting train and test sets. It can easily be done with pandas if we do a regular train-test split.

However, if you want to do cross validation, it will be tedious to use Pandas. The pipelines of scikit-learn library provide a more practical and easier way.

The scope of pipelines are quite broad. You can also add other preprocessing techniques in a pipeline such as a scaler for numerical values. Using pipelines allows automating certain tasks and thus optimizing processes.

If you’re new to data science, here’s a good place to start

One of the most well-known and essential sub-fields of data science is machine learning. The term machine learning was first used in 1959 by IBM researcher Arthur Samuel. From there, the field of machine learning gained much interest from others, especially for its use in classifications.

When you start your journey into learning and mastering the different aspects of data science, perhaps the first sub-field you come across is machine learning. Machine learning is the name used to describe a collection of computer algorithms that can learn and improve by gathering information while they are running.

Any machine learning algorithm is built upon some data. Initially, the algorithm uses some “training data” to build an intuition of solving a specific problem. Once the algorithm passes the learning phase, it can then use the knowledge it gained to solve similar problems based on different datasets.

In general, we categorize machine learning algorithms into 4 categories:

1. Supervised algorithms: Algorithms that involve some supervision from the developer during the operation. To do that, the developer labels the training data and set strict rules and boundaries for the algorithm to follow.
2. Unsupervised algorithms: Algorithms that do not involve direct control from the developer. In this case, the algorithms’ desired results are unknown and need to be defined by the algorithm.
3. Semi-supervised algorithms: Algorithms that combines aspects of both supervised and unsupervised algorithms. For example, not all training data will be labeled, and not all rules will be provided when initializing the algorithm.
4. Reinforcement algorithms: In these types of algorithms, a technique called exploration/exploitation is used. The gest of it is simple; the machine makes an action, observe the outcomes, and then consider those outcomes when executing the next action, and so on.

Each of these categories is designed for a purpose; for example, supervised learning is designed to scale the training data’s scope and make predictions of future or new data based on that. On the other hand, unsupervised algorithms are used to organize and filter data to make sense of it.

Under each of those categories lay various specific algorithms that are designed to perform certain tasks. This article will cover 5 basic algorithms every data scientist must know to cover machine learning basics.

№1: Regression

Regression algorithms are supervised algorithms used to find possible relationships among different variables to understand how much the independent variables affect the dependent one.

You can think of regression analysis as an equation, For example, if I have the equation y = 2x + z, y is my dependant variable, and x,z are the independent ones. Regression analysis finds how much do x and z affect the value of y.

The same logic applies to more advanced and complex problems. To adapt to the various problems, there are many types of regression algorithms; perhaps the top 5 are:

1. Linear Regression: The simplest regression technique uses a linear approach for featuring the relationship between the dependent (predicted) and independent variables (predictors).
2. Logistic Regression: This type of regression is used on binary dependent variables. This type of regressing is widely used to analyze categorical data.
3. Ridge Regression: When the regression model becomes too complex, ridge regression corrects the model’s coefficients’ size.
4. Lasso Regression: Lasso (Least Absolute Shrinkage Selector Operator) Regression is used to select and regularize variables.
5. Polynomial Regression: This type of algorithm is used to fit non-linear data. Using it, the best prediction is not a straight line; it is a curve that tries to fit all data points.

№2: Classification

Classification in machine learning is the process of grouping items into categories based on a pre-categorized training dataset. Classification is considered a supervised learning algorithm.

These algorithms use the training data’s categorization to calculate the likelihood that a new item will fall into one of the defined categories. A well-known example of classification algorithms is filtering incoming emails into spam or not-spam.

There are different types of classification algorithms; the top 4 ones are:

1. K-nearest neighbor: KNN is an algorithm that uses training datasets to find the k closest data points in some datasets.
2. Decision trees: You can think of it as a flow chart, classifying each data points into two categories at a time and then each to two more and so on.
3. Naive Bayes: This algorithm calculates the probability that an item falls under a specific category using the conditional probability rule.
4. Support Vector Machine (SVM): In this algorithm, the data is classified based on its degree of polarity, which can go beyond the X/Y prediction.

№3: Ensembling

Ensembling algorithms are supervised algorithms made of combining the prediction of two or more other machine learning algorithms to produce more accurate results. Combining the results can either be done by voting or averaging the results. Voting is often used during classification and averaging during regression.

Ensembling algorithms have 3 basic types: Bagging, Boosting, and Stacking.

1. Bagging: In bagging, the algorithms are run in parallel on different training sets, all equal in size. All algorithms are then tested using the same dataset, and voting is used to determine the overall results.
2. Boosting: In the case of boosting, the algorithms are run sequentially. Then the overall results are chosen using weighted voting.
3. Stacking: From the name, stacking has two-level stacked on top of each other, the base level is a combination of algorithms, and the top level is a meta-algorithm based on the base level results.

№4: Clustering

Clustering algorithms are a group of unsupervised algorithms used to group data points. Points within the same cluster are more similar to each other than to points in different clusters.

There are 4 types of clustering algorithms:

1. Centroid-based Clustering: This clustering algorithm organizes the data into clusters based on initial conditions and outliers. k-means is the most knowledgeable and used centroid-based clustering algorithm.
2. Density-based Clustering: In this clustering type, the algorithm connects high-density areas into clusters creating arbitrary-shaped distributions.
3. Distribution-based Clustering: This clustering algorithm assumes the data is composed of probability distributions and then clusters the data into various versions of that distribution.
4. Hierarchical Clustering: This algorithm creates a tree of hierarchical data clusters, and the number of clusters can be varied by cutting the tree at the correct level.

№5: Association

Association algorithms are unsupervised algorithms used to discover the probability of some items to occur together in a specific dataset. It is mostly used in the market-basket analysis.

The most used association algorithm is Apriori.

The Apriori algorithm is a mining algorithm used commonly used in transactional databases. Apriori is used to mine frequent itemsets and generate some association rules from those item sets.

For example, if a person buys milk and bread, then they are likely to also get some eggs. These insights are built upon previous purchases from various clients. Association rules are then formed according to a specific threshold for confidence set by the algorithm based on how frequently these items are brought together.

Final Thoughts

Machine learning is one of the most famous, well-researched sub-field of data science. New machine learning algorithms are always under development to reach better accuracy and faster execution.

Regardless of the algorithm, it can generally be categorized as one of four categories: supervised, unsupervised, semi-supervised, and reinforced algorithms. Each one of these categories holds many algorithms that are used for different purposes.

In this article, I have gone through 5 types of supervised/ unsupervised algorithms that every machine learning beginner should be familiar with. These algorithms are well-studied and widely-used that you only need to understand how to use it rather than how to implement it.

Most famous Python machine learning modules — such as Scikit Learn — contain a pre-defined version of most — if not all — of these algorithms.

So,

My advice is, understand the mechanic, and master the usage and start building.